Unlocking the Secrets of the Circumference of a Circle
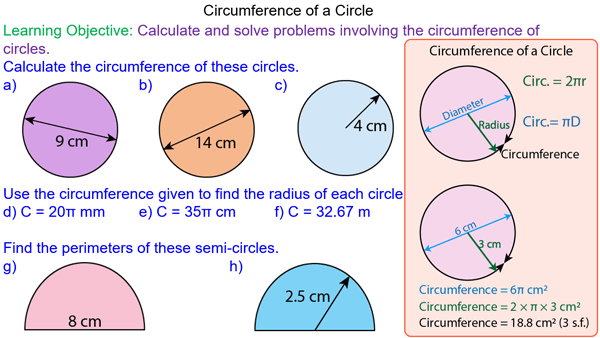
Key Takeaways
- The circumference is the distance around a circle.
- It can be calculated using the formula C = 2πr or C = πd.
- Understanding circumference is crucial in various real-world applications, from engineering to everyday tasks.
When you think of circles, what comes to mind? Perhaps it’s the shape of a pizza, the rim of a bicycle wheel, or even the orbit of a planet. All these circular objects have one thing in common: they have a circumference. Understanding the circumference of a circle is not just an academic exercise; it’s a concept that has practical applications in our daily lives. In this article, we will delve deep into the concept of the circumference of a circle, exploring its definition, formulas, and real-world applications.
What is the Circumference of a Circle?
The circumference of a circle is the linear distance around its edge. Imagine wrapping a piece of string around a circular object and then measuring the length of the string; that’s the circumference. It’s akin to the perimeter of a polygon, but since a circle is a continuous curve, we use the term “circumference” instead.

Understanding the Formula
The formula for calculating the circumference of a circle is straightforward, yet it holds a world of mathematical beauty. There are two primary formulas used to find the circumference:
- C = 2πr – where C is the circumference, r is the radius of the circle, and π (pi) is approximately 3.14159.
- C = πd – where d is the diameter of the circle. Since the diameter is twice the radius (d = 2r), both formulas are essentially the same.
Why is Pi (π) So Important?
Pi (π) is a mathematical constant that represents the ratio of the circumference of any circle to its diameter. This ratio is constant for all circles and is approximately 3.14159. Pi is an irrational number, meaning it cannot be exactly expressed as a simple fraction, and its decimal representation goes on forever without repeating. Pi is not just a number; it’s a bridge that connects the linear and the circular world.
Real-World Applications of Circumference
Understanding the circumference of a circle is not just an abstract mathematical concept; it has numerous practical applications:
1. Engineering and Construction
Engineers and architects frequently use the concept of circumference when designing circular structures, such as domes and arches. Knowing the circumference helps in determining the amount of materials needed and ensuring structural integrity.
2. Everyday Measurements
Whether you’re measuring the distance around a tree trunk or calculating the length of a fence needed to enclose a circular garden, the circumference is a handy measure. It simplifies tasks and ensures accuracy in everyday measurements.
3. Astronomy and Space Science
In the vastness of space, celestial bodies such as planets and stars often have circular orbits. Calculating the circumference of these orbits helps astronomers understand distances and movements within our universe.
Exploring the Relationship Between Diameter, Radius, and Circumference
To fully grasp the concept of circumference, it’s essential to understand the relationship between a circle’s diameter, radius, and circumference. The diameter of a circle is the longest distance across it, passing through the center. The radius is half the diameter, extending from the center to any point on the circle’s edge. The circumference, as mentioned earlier, is the distance around the circle.
By knowing any one of these three measurements, you can easily calculate the others using the formulas:
- If you know the radius, multiply it by 2π to find the circumference.
- If you know the diameter, multiply it by π to get the circumference.
- If you have the circumference, divide it by π to find the diameter, and then divide the diameter by 2 to get the radius.
A Deeper Dive into Pi (π)
Pi is more than just a number used in geometry; it has fascinated mathematicians for centuries. It appears in various mathematical contexts, including trigonometry, calculus, and complex numbers. Its ubiquity and mystery have made it a subject of intrigue and study, with countless mathematicians attempting to calculate its digits to unprecedented lengths.
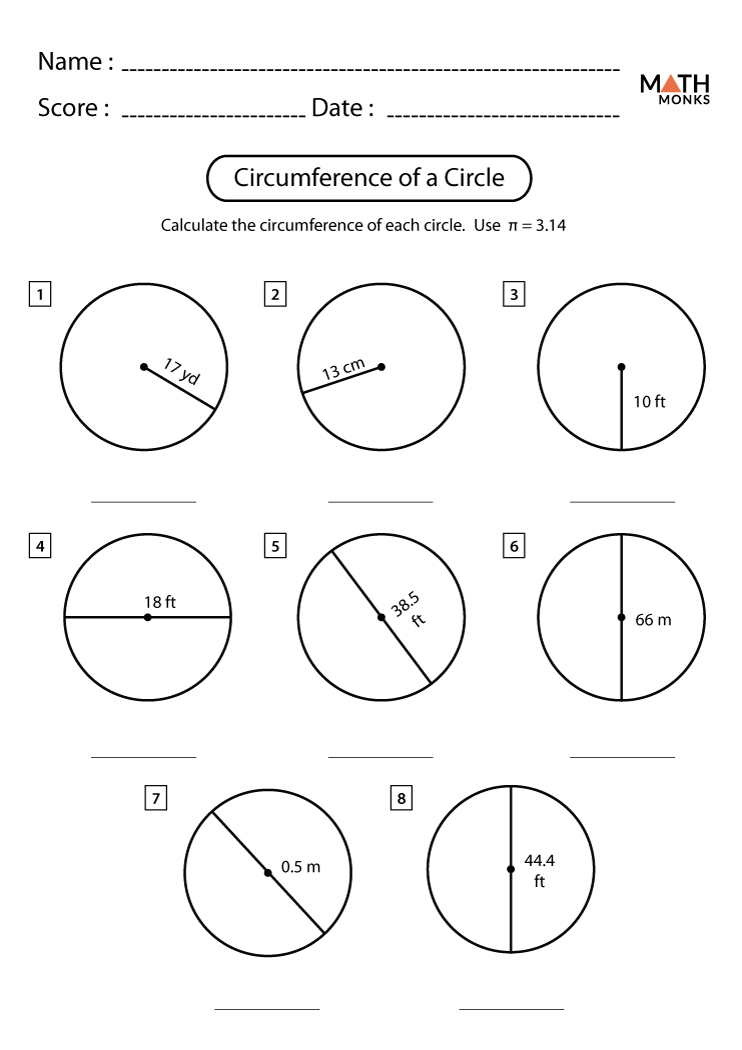
The circumference of a circle is a fundamental concept in mathematics with far-reaching applications. From the simple act of measuring a circular object to the complexities of engineering and space science, understanding the circumference is essential. By mastering the formulas and grasping the relationship between diameter, radius, and circumference, you unlock a deeper appreciation for the circular forms that populate our world.
Incorporating this knowledge into practical tasks not only enhances precision but also enriches your mathematical toolkit. So, the next time you encounter a circle, remember the elegance of its circumference and the mathematical principles that bring it to life.